Accelerate Electronics Verification and Compliance — Deploy Pilot EDFS in Weeks, Not Months
-
EDFS - Pilot Edition (DFS4 + DFS5 limited)
Target: SBIR teams, evaluations
Features:
Core graph execution
RF/MW workflows
MXD disk
Reporting
Price: $25,000 / year / organization
-
EDFS PRO - Professional Edition
Target: Defense contractors, semiconductor R&D
Features:
Full DFS stack
Subsystem flattening
Regression/baselines
Script editor + REPL
Price: $75,000 / year / organization
-
EDFS Enterprise Edition
Target: primes, fabs, labs
Features:
Multi-team deployment
HIL hooks
Priority support
Custom block development
Price: $150,000–$300,000 / year

Cogn-Tex: Electronics Design Flow Studio (EDFS)
Integrated Verification & Automation Platform for Commercial Electronics Development.
Electronic DFS empowers small and medium electronics companies to automate design verification, reduce rework cycles, and accelerate product launches with a scalable pilot licensing model.
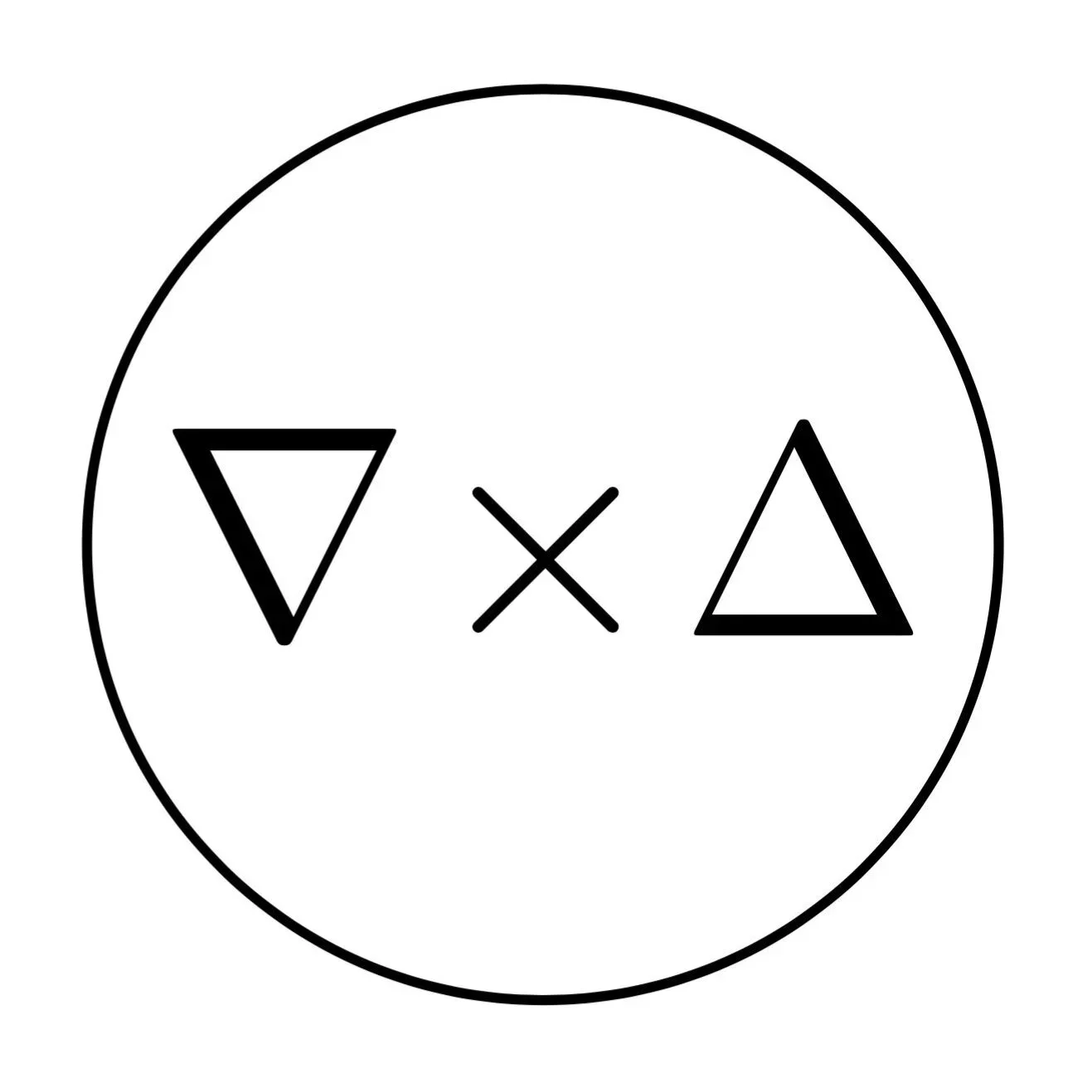
This diagram represents the closed-loop EDFS execution core. The inverted triangle (▽) denotes incoming uncertainty from datasheets, EDA tools, and EM solvers; the intersection phase (✕) occurs within the RF-Lab DFS-5 Core, where models, simulations, and measurements converge; and the encapsulated system (◯) reflects a stabilized, self-consistent simulation environment producing validated RF behavior and actionable parameters.

MAXDI RESEARCH
Exploration Driven by
Mxd-Cogn: Emergent Deformed Field System (EDFS)

mxd-cogn: A theory of Mixed-domain and Mixed-depth
-
n the textbook, MXD-COGN is built on three structural moves:
State is not a point; it is cross-domain closure.
You define an MXD-COGN state ΣΣ as an equivalence class of representations across multiple domain fibers, bound together by “inferential consistency” (bounded-error mappings between domains). Concretely, Σ={ri∈FDi∣∀i,j, ri∼rj}Σ={ri∈FDi∣∀i,j, ri∼rj}, so “having a state” means “maintaining inferential closure across domains,” not “occupying a single configuration.” MXD-COGN-CompleteInference is operator-valued and generically non-commutative.
Inference is represented by domain-to-domain operators Ii→j:FDi→FDjIi→j:FDi→FDj, with an explicit axiom that these operators generally do not commute. The non-commutativity is treated as structural (e.g., irreversible compression/abstraction), not as a quantum postulate. MXD-COGN-Complete“Deformation” is the control knob; coherence is the order parameter.
Operators become Ii→j(λ)Ii→j(λ) under a real deformation parameter λ≥0λ≥0 that captures increasing approximation, mismatch, latency, compression, etc. MXD-COGN-Complete
Global coherence is summarized by the order parameter Φ(Σ)∈[0,1]Φ(Σ)∈[0,1], explicitly described as non-probabilistic and macroscopic. MXD-COGN-Complete
In Chapter 3, you then formalize ΦΦ as a loop-aggregated functional of closure errors (via weighted inference cycles), making “coherence” mathematically concrete as closure-under-composition behavior. MXD-COGN-CompleteThat is the “deformed controlled inference” core: deform operators, measure closure, and control the system by staying inside coherence/stability basins.
-
What MXD-COGN can legitimately claim (operationally):
“Superposition-like behavior” corresponds to an inference configuration that has not yet been fixed by deformation/closure constraints—i.e., the system maintains multiple partially consistent representational candidates across fibers and operators, and the act of committing (your “deformation fixing”) selects a stable, closed equivalence class ΣΣ. This is exactly the role you assign in Appendix J when you say “wavefunction ΨΨ” is replaced by “inference configuration,” and “measurement collapse” is replaced by “deformation fixing.” MXD-COGN-CompleteHow that ties to your formal Chapter 2 state definition:
Because ΣΣ is an equivalence class defined by cross-domain inferential consistency, “pre-fixation” is naturally represented as: the system has not yet formed (or cannot yet maintain) a single closure-consistent equivalence class across the relevant fibers. MXD-COGN-CompleteWhat MXD-COGN should not claim (if you want to stay technically tight):
Not that a physical system is literally “in two ontic states at once.”
Not that MXD-COGN derives the Born rule.
Not that “superposition” is a physical wavefunction in this framework. Appendix J is clear that the wavefunction terminology is replaced, not preserved. MXD-COGN-Complete
-
Appendix J gives you the cleanest sentence you can use in public:
Entanglement → coupled inference loops. MXD-COGN-CompleteUnder the core theory, this becomes:
Two subsystems (or domains) are “entangled” when their closure errors and stability cannot be analyzed independently because the decisive inference cycles traverse both (cross-coupled loops). In other words, the system’s coherence functional ΦΦ is dominated by joint loops, so any attempt to assign separate local “states” breaks closure. This is consistent with the fact that ΦΦ is built by aggregating loop closure errors over admissible cycles. MXD-COGN-Complete
This gives you a direct analogue of the entanglement signature that matters experimentally: strong, non-factorizable correlations. MXD-COGN’s “correlations” are not probabilistic primitives; they arise because the graph of inference operators creates inseparable closure constraints across domains/subgraphs.
-
In MXD-COGN, “quantum-inspired” language is translated into graph-native inference geometry: an MXD-COGN state ΣΣ is not a point but an equivalence class of cross-domain representations satisfying inferential consistency (closure), with inference realized by generally non-commuting domain operators Ii→j(λ)Ii→j(λ) under deformation λλ. MXD-COGN-Complete Superposition is therefore modeled as an unfixed inference configuration—multiple partially consistent representational candidates across fibers that have not yet been stabilized into a single closure-consistent equivalence class—while “measurement collapse” is reinterpreted as deformation fixing (commitment/closure under constraints). MXD-COGN-Complete Entanglement is modeled as coupled inference loops: the system’s global coherence ΦΦ depends on joint cycles spanning subsystems, so correlations are structurally non-factorizable because closure errors propagate through shared loops rather than separable local states. MXD-COGN-Complete